A continuación presentamos 4 teoremas que nos ayudarán a resolver muchos problemas de geometría que aparecen en las etapas eliminatorias de las Olimpiadas de Matemática.
(Esta entrada participa en el «Carnaval de Matemáticas» y cuyo blog anfitrión es Gaussianos).
1. Teorema de Ptolomeo.
En todo cuadrilátero inscribible en una circunferencia (cíclico), la suma de los productos de los pares de lados opuestos es igual al producto de sus diagonales.
En la figura siguiente:

tendríamos que
\[AC \cdot BD = AB \cdot CD + BC \cdot AD \]
Demostración:
Considere la siguiente figura:
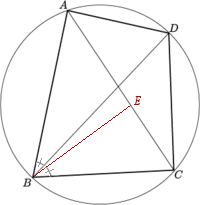
Sea \( E\) sobre la diagonal \( AC\) tal que
- \( \widehat{CBE} = \widehat{ABD}\), por construcción,
- \( \widehat{BCA} = \widehat{BDA}\), por subtender el mismo arco.
Entonces \( \Delta BCE \sim \Delta BDA\), por criterio \( AAA\), y de esta semejanza obtenemos:
\[ \label{ptol:eq1} \tag{1} \displaystyle { \frac{BC}{CE} = \frac{BD}{AD} \Rightarrow BC \cdot AD = CE \cdot BD } \]
Y como \( \Delta BAE \sim \Delta BDC\) (queda como ejercicio dar el razonamiento) entonces:
\[ \label{ptol:eq2} \tag{2} \displaystyle { \frac{AB}{BD} = \frac{AE}{CD} \Rightarrow AB \cdot CD = BD \cdot AE } \]
Sumando \eqref{ptol:eq1} y \eqref{ptol:eq2} se tiene que:
\[ AD \cdot BC + AB \cdot CD = BD \cdot CE + BD \cdot AE\]
\[ \Rightarrow AD \cdot BC + AB \cdot CD = BD \cdot (CE + AE)\]
\[ \Rightarrow AD \cdot BC + AB \cdot CD = BD \cdot AC \blacksquare \]
2. Teorema de Pierre Varignon.
La figura formada cuando se unen en el orden dado los puntos medios de un cuadrilátero convexo es un paralelogramo, y su área es la mitad de la del cuadrilátero original.
3. Teorema de Ceva.
Tres rectas que pasan por los vértices de un triángulo son concurrentes si y sólo si el producto de las razones en que dividen los lados opuestos es igual a 1.
Demostración:
Considere la siguiente figura:

Tenemos que:
\[ \displaystyle \frac{AF}{FB} = \displaystyle \frac{(OAF)}{(OFB)} = \displaystyle \frac{(CAF)}{(CFB)} = \displaystyle \frac{(CAF) – (OAF)}{(CFB) – (OFB)} \]
\[ \Rightarrow \displaystyle \frac{AF}{FB} = \displaystyle \frac{(COA)}{(COB)} \]
Del mismo modo, se tiene también:
\[ \displaystyle \frac{BD}{DC} = \displaystyle \frac{(AOB)}{(AOC)} \]
\[ \displaystyle \frac{CE}{EA} = \displaystyle \frac{(BOC)}{(BOA)} \]
entonces:
\[ \displaystyle \frac{AF}{FB} \cdot \displaystyle \frac{BD}{DC} \cdot \displaystyle \frac{CE}{EA} = \displaystyle \frac{(COA)}{(COB)} \cdot \displaystyle \frac{(AOB)}{(AOC)} \cdot \displaystyle \frac{(BOC)}{(BOA)} = 1 \blacksquare\]
4. Teorema de Menelao.
Tres puntos sobre las rectas \( BC\), \( AC\) y \( AB\) son colineales si y sólo si el producto de las razones en que dividen a los lados del triángulo \( ABC\) es 1.
En la figura siguiente

esto sería:
\[ \displaystyle \frac{AE}{EC} \cdot \displaystyle \frac{CD}{DB} \cdot \displaystyle \frac{BF}{FA} = 1 \]

Muchas gracias! esta muy bueno 🙂