Los siguientes ejercicios se componen de una pregunta básica, seguida de varias posibles respuestas, de las cuales sólo una es la verdadera.
La recomendación es efectuar todas las operaciones necesarias (como si fuera una pregunta de desarrollo) antes de marcar una de las opciones.
Si no encuentra la manera de resolver el problema, escriba qué exactamente fue lo que le impidió llegar a la respuesta.
1. El valor numérico de la expresión \( \left[ \left( \displaystyle \frac{ 4v^{-2}x^{-3}y^{2} }{ 8v^{-3}x^{-2}y } \right)^{-2} \right]^{-1} \), si \(v=2\), \(y=-\frac{1}{2}\), \(x=-\frac{1}{4}\), es:
A) -1
B) 8
C) \(-\frac{1}{8}\)
D) 4
2. Una finca de 5 hectáreas tiene el 22% de su superficie sembrada de césped y el resto de diversos cultivos. ¿Cuántos \(m^{2}\) de césped y cuántos de otros cultivos tiene la finca?
A) 11000 \(m^{2}\) de césped; 39000 \(m^{2}\) de otros cultivos
B) 1100 \(m^{2}\) de césped; 3900 \(m^{2}\) de otros cultivos
C) 22727 \(m^{2}\) de césped; 27273 \(m^{2}\) de otros cultivos
D) 2272 \(m^{2}\) de césped; 2727 \(m^{2}\) de otros cultivos
3. Si \(H, K, M, N\) son números positivos, tales que \(K>M, N>H\), ¿cuál de los siguientes planteamientos es cierto?
I. \(K + H > M + N\)
II. \(K + N > M + H\)
II. \(K + M > N + H\)
A) I solamente
B) II solamente
C) I y II
D) I, II y III
4. El 70% de los habitantes de un país habla un idioma y el 60% de la misma población habla otro idioma. ¿Qué porcentaje de la población habla los dos idiomas, sabiendo que cada habitante habla al menos uno de ellos?
A) 70%
B) 80%
C) 30%
D) 100%
5. El área de un círculo mide \(10 cm^{2}\). Si su radio se reduce a \(\frac{1}{3}\) de su longitud, entonces el área, con respecto a su medida original, se ha reducido a
A) \(\frac{1}{3}\)
B) \(\frac{1}{9}\)
C) \(\frac{1}{6}\)
D) \(\frac{1}{12}\)
6. Si el radio de un círculo se incrementa en 100%, el área incrementará
A) 100%
B) 200%
C) 300%
D) 400%
7. En una promoción el precio de un artículo es rebajado en un 12% de su precio original. Si el artículo se vendió en $220, entonces su precio original corresponde a
A) $275
B) $250
C) $1100
D) $470
8. Sea \(P(x)=5x^{4}+9x^{2}-6x-8\) y \(T(x)=2x^{4}+8x^{3}+9x^{2}-16x-3\). Si \(P(x)-Q(x)=T(x)\), el polinomio \(Q(x)\) corresponde a
A) \(3x^{4}+8x^{3}+18x^{2}-22x-11\)
B) \(8x^{3}-3x^{4}+5-10x\)
C) \(3x^{4}-8x^{3}+10x-5\)
D) \(7x^{4}+8x^{3}+18x^{2}-22x-11\)
9. Si \(a = \frac{1}{4}\) y \(b = \frac{-1}{2}\) entonces el valor numérico de \((a+b)(a^{2}-ab+b^{2})\) es
A) \(\frac{9}{64}\)
B) \(\frac{9}{8}\)
C) \(\frac{-7}{64}\)
D) \(\frac{-7}{8}\)
10. Al multiplicar \(x^{5}\); \(x + \frac{1}{x}\); \(1 + \frac{2}{x} + \frac{3}{x^{2}}\), el grado del polinomio resultante es
A) 2
B) 3
C) 8
D) 6
11. Si el 5% de una cantidad es \(«t»\), la cantidad es
A) \(5t\)
B) \(20t\)
C) \(\frac{t}{20}\)
D) \(\frac{t}{5}\)
12. Se tiene que \(a+b+c=104\). Entonces el total \((5 – a) + (8 – b) + (9 -c)\) es
A) 110
B) 98
C) -126
D) -82
13. El número de veces que pasa el minutero de un reloj por un mismo punto de un día es
A) 12
B) 24
C) 1440
D) 86400
14. El conjunto de los números reales cuya mitad más dos está comprendida entre -20 y 20 satisfacen la condición:
A) -44 < x < 36
B) -44 < x < 44
C) -8 < x < 10
D) -8 < x < 8
15. Las fracciones equivalentes a \(\frac{20}{30}\) que tienen denominador positivo y menor que 12, son las siguientes
A) \(\frac{2}{3}\), \(\frac{4}{6}\), \(\frac{12}{18}\)
B) \(\frac{2}{3}\), \(\frac{4}{9}\), \(\frac{3}{4}\), \(\frac{15}{10}\)
C) \(\frac{2}{3}\), \(\frac{4}{6}\), \(\frac{6}{9}\), \(\frac{8}{12}\)
D) \(\frac{2}{3}\), \(\frac{4}{6}\), \(\frac{6}{9}\)
16. En un colegio diurno de 810 alumnos, los \(\frac{5}{9}\) estudian en la mañana. Entonces el número de estudiantes que estudian en la tarde es
A) 450
B) 360
C) 162
D) 203
17. En una finca sus \(\frac{2}{5}\) partes están sembradas de café y la tercera parte del resto está sembrada de árboles frutales. Si el resto de la finca está desocupada, entonces podemos afirmar que la finca tiene ocupada
A) \(\frac{1}{5}\)
B) \(\frac{2}{5}\)
C) \(\frac{3}{5}\)
D) \(\frac{4}{5}\)
18. Si \(\frac{a}{b}\) corresponde a una fracción propia y \(\frac{c}{d}\) a una fracción impropia, siendo \(a, b, c, d\) enteros positivos, entones podemos asegurar que
A) \(c > a\) y \(d > b\)
B) \(c < a\) y \(b > d\)
C) \(ad > bc\)
D) \(ad < bc\)
19. Una expresión equivalente a \((2a – 3b)x^{2} – (2a + 3b)x^{2}\) es
A) \(18b^{2}\)
B) 0
C) \(-24ab\)
D) \(-18b^{2}\)
20. Un carpintero corta una tabla de 50 cm de largo en dos piezas. Una de las piezas es 10 cm más larga que la otra. Entonces la longitud de la pieza más corta es
A) 15 cm
B) 10 cm
C) 30 cm
D) 20 cm
21. Sean \(p(x) = 2 – x\), \(q(x) = 4 + 2x + x^{2}\) el producto \(p(x)q(x)\) es igual al polinomio
A) \(x^{3} – 8\)
B) \(8 + 3x^{2} + x^{3}\)
C) \(8 + x^{3}\)
D) \(8 – x^{3}\)
22. Si \(x = 1 + 2^{p}\), \(y = 1 + 2^{-p}\), entonces \(«y»\) en términos de \(«x»\) es
A) \(\displaystyle \frac{ x+1 }{ x-1 }\)
B) \(\displaystyle \frac{ x+2 }{ x-1 }\)
C) \(\displaystyle \frac{ x }{ x-1 }\)
D) \(\displaystyle \frac{ x-1 }{ x }\)
23. La expresión \( \left( \displaystyle \frac{ x^{2} + 1 }{ x } \right) \left( \displaystyle \frac{ y^{2} + 1 }{ y } \right) + \left( \displaystyle \frac{ x^{2} – 1 }{ y } \right) \left( \displaystyle \frac{ y^{2} – 1 }{ x } \right) \) equivale a
A) 1
B) \(2x^{2}y^{2} + 2\)
C) \(2xy + \frac{ 2 }{ xy } \)
D) \(\frac{ 2x }{ y } + \frac{ 2y }{ x } \)
24. La expresión \(2^{-(2x+1)} – 2^{-(2x-1)} + 2^{-2x}\), equivale a
A) \(2^{-2x}\)
B) \(2^{-(2x-1)}\)
C) \(-2^{-(2x+1)}\)
D) \(2\)
25. Alberto puede hacer un trabajo en 9 días. Bernardo es un 50% más eficiente que Alberto. El número de días que Bernardo emplea para hacer el mismo trabajo es
A) \(13 \frac{ 1 }{ 2 } \)
B) \(4 \frac{ 1 }{ 2 } \)
C) 6
D) 3
26. El señor Aguilar tiene una bicicleta que vale $10000. La vende al señor Bermudez con una ganancia del 10%. El señor Bermudez la vende nuevamente al señor Aguilar con una pérdida del 10%. Entonces:
A) El señor Aguilar no gana nada.
B) El señor Aguilar pierde $900 en el negocio.
C) El señor Aguilar pierde $1100 en el negocio.
D) El señor Aguilar gana $1100 en el negocio.
27. Si h hombres hacen un trabajo en d días, y asumiendo que todos los hombres trabajan al mismo ritmo, entonces (h + v) hombres pueden hacer el mismo trabajo en
A) (d + v) días
B) (d – v) días
C) \(\frac{ d }{ (h + v) } \) días
D) \(\frac{ hd }{ (h + v) } \) días
28. Descuentos sucesivos de 10% y 20% son equivalentes a un descuento único de
A) 30%
B) 15%
C) 72%
D) 28%
29. Cuatro veces la mitad de la edad de una persona es 32 años. La edad de la persona es
A) 10 años
B) 16 años
C) 32 años
D) 64 años
30. Los perros pueden escuchar sonidos a una distancia 10 veces mayor que los humanos. Un perro puede escuchar un sonido a 270 metros de distancia. La distancia a la cual podría un hombres escuchar este sonido es
A) 2.7 metros
B) 27 metros
C) 270 metros
D) 2700 metros
31. En un curso universitario de 90 estudiantes, la tercera parte de los alumnos tiene 18 años, la mitad tiene 19 años y los restantes tienen 20 años. La suma total de sus edades en años es
A) 1695
B) 1705
C) 1895
D) 2115
32. En una reunión de 15 personas, cada una da la mano a todos los demás, ¿cuántos apretones de manos hay?
A) 210
B) 196
C) 195
D) 105
33. En una promoción el precio de un artículo es rebajado en un 13%. Si el artículo se vendió en $217.50 el precio original es
A) $204.50
B) $230.50
C) $250
D) $275
34. En un camión que distribuye refrescos, se pueden colocar 15 cajas a lo largo, 10 a lo ancho, y una sobre otra se pueden colocar (por columna) 12 cajas. ¿Cuántas cajas de refrescos transporta el camión si se carga a una tercera parte de su capacidad?
A) 500
B) 600
C) 1200
D) 1800
35. Si \(\frac{ a }{ b } \in \mathbb{Q}\) tal que \(0 < \frac{ a }{ b } < 1\) entonces una proposición verdadera corresponde a
A) \((\frac{ a }{ b })^{2} < (\frac{ a }{ b })^{3}\)
B) \((\frac{ a }{ b })^{2} > (\frac{ a }{ b })^{3}\)
C) \((\frac{ a }{ b })^{2} > 1\)
D) \((\frac{ a }{ b })^{2} > \frac{ a }{ b }\)
36. Un tren marcha a una velocidad de 54 Km/h. Al cabo de \( \frac{ 5 }{ 3 } \) de hora ha recorrido
A) 90 Km
B) 32.4 Km
C) 74 Km
D) 10.8 Km
37. El resultado de \(-(3x^{2}+7x) – 2[3x – 2x(9 – 3x)]\) es
A) \(23x – 15x^{2}\)
B) \(-(15x^{2} + 9x)\)
C) \(9x^{2} + 23x\)
D) \(15x^{2} – 23x\)
38. El promedio de tres pruebas cortas de matemática tienen un valor de 40% de la calificación final. Si yo obtuve el 32% del 40% ¿qué promedio tengo en las tres pruebas cortas?
A) 12.8
B) 12.5
C) 80
D) 70
39. La factorización completa de un número P es \(a^{2}bc^{3}\) y la factorización completa de un número R es \(a^{3}b^{2}c^{2}\), entonces el M.C.M. entre P y R es el siguiente
A) \(a^{2}bc^{2}\)
B) \(abc\)
C) \(a^{3}b^{2}c^{3}\)
D) \(a^{5}b^{3}c^{5}\)
40. Si al cuadrado de un número de dos dígitos se el quita el cuadrado del número formado por los dos dígitos en orden invertido, entonces el resultado no es siempre divisible por
A) 9
B) 11
C) el producto de los dígitos
D) la suma de los dígitos
41. El número de dígitos de \(N = 2^{12} \bullet 5^{8}\) es
A) 10
B) 9
C) 12
D) 11
42. Si la operación * en el conjunto de los números reales positivos se define por \(a * b = \displaystyle \frac{a – 4ab}{2-b}\), entonces \((2 * 3) * 4\) es igual a
A) 22
B) 24
C) 165
D) 12
43. Una casa y una tienda se vendieron por $12000 cada una. La casa se vendió con un 20% menos del costo y la tienda con una ganancia del 20% del costo. La transacción total dio por resultado
A) Ni pérdida ni ganancia
B) Una pérdida de $1000
C) Una ganancia de $1000
D) Una ganancia de $2000
44. Una ama de casa ahorra $250 en la compra de un vestido. Si gastó $2500 en el vestido, ahorró aproximadamente
A) 8%
B) 9%
C) 10%
D) 11%
45. Si \( \frac{1}{x} – \frac{1}{y} = \frac{1}{z} \), entonces \(«z»\) es igual a
A) \(y – x\)
B) \(x – y\)
C) \(\frac{xy}{y – x}\)
D) \(\frac{y – x}{xy}\)
46. Si \( x^{-1} – 1 \) es dividido por \(x – 1\) el cociente es
A) 1
B) \( \frac{1}{x – 1}\)
C) \( \frac{1}{x}\)
D) \( -\frac{1}{x}\)
47. Cuando simplificamos \((x^{-1} + y^{-1})^{-1}\) se obtiene
A) \( x + y \)
B) \( \frac{xy}{x + y}\)
C) \( xy \)
D) \( -\frac{x + y}{xy}\)
48. Cuando se simplifica y se expresa con exponentes negativos, la expresión \((x + y)^{-1} (x^{-1}+y^{-1})\) se obtiene
A) \( x^{-2} + 2x^{-1}y^{-1} + y^{-2} \)
B) \( x^{-2} + 2^{-1}x^{-1}y^{-1} + y^{-2} \)
C) \( x^{-1}y^{-1} \)
D) \( x^{-2} + y^{-2} \)
49. La fracción \( \displaystyle \frac{a^{-4} – b^{-4}}{a^{-2} – b^{-2}}\) es igual a
A) \( a^{-6} – b^{-6} \)
B) \( a^{-2} – b^{-2} \)
C) \( a^{-2} + b^{-2} \)
D) \( a^{2} – b^{2} \)
50. Considere la siguiente representación gráfica de la circunferencia C de centro P:
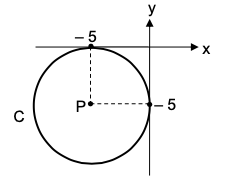
De acuerdo con la información anterior, la ecuación de esa circunferencia corresponde a
A) \( (x-5)^{2} + (y-5)^{2} = 10 \)
B) \( (x+5)^{2} + (y+5)^{2} = 10 \)
C) \( (x-5)^{2} + (y-5)^{2} = 25 \)
D) \( (x+5)^{2} + (y+5)^{2} = 25 \)
Compilación original por Miguel Arias Vilchez,
exepto el problema 50 que fue tomado de una práctica para las pruebas de Bachillerato del MEP.

